Poisson kernel
In potential theory, the Poisson kernel is an integral kernel, used for solving the two-dimensional Laplace equation, given Dirichlet boundary conditions on the unit disc. The kernel can be understood as the derivative of the Green's function for the Laplace equation. It is named for Siméon Poisson.
The Poisson kernel is important in complex analysis because its integral against a function defined on the unit circle — the Poisson integral — gives the extension of a function defined on the unit circle to a harmonic function on the unit disk. By definition, harmonic functions are solutions to Laplace's equation, and, in two dimensions, harmonic functions are equivalent to meromorphic functions. Thus, the two-dimensional Dirichlet problem is essentially the same problem as that of finding a meromorphic extension of a function defined on a boundary.
Poisson kernels commonly find applications in control theory and two-dimensional problems in electrostatics. In practice, the definition of Poisson kernels are often extended to n-dimensional problems.
Contents |
Two-dimensional Poisson kernels
On the unit disc
In the complex plane, the Poisson kernel for the unit disc is given by
This can be thought of in two ways: either as a function of r and θ, or as a family of functions of θ indexed by r.
If 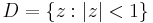 is the unit disc in C, and if f is a continuous function from the unit circle
is the unit disc in C, and if f is a continuous function from the unit circle 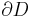 into R, then the function u given by
into R, then the function u given by
or equivalently by
is harmonic in D, and extends to a continuous function on 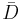 that agrees with f on the boundary of the disc.
that agrees with f on the boundary of the disc.
It is common to restrict oneself to functions which are either square integrable or p-integrable on the unit circle. When one also asks for the harmonic extension to be holomorphic, then the solutions are elements of a Hardy space. In particular, the Poisson kernel is commonly used to demonstrate the equivalence of the Hardy spaces on the unit disk, and the unit circle.
In the study of Fourier series the Poisson kernel arises in the study of Abel means for a Fourier series, and gives an example of a summability kernel (Katznelson 1976)
On the upper half-plane
The unit disk may be conformally mapped to the upper half-plane by means of certain Möbius transformations. Since the conformal map of a harmonic function is also harmonic, the Poisson kernel carries over to the upper half-plane. In this case, the Poisson integral equation takes the form
for 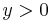 . The kernel itself is given by
. The kernel itself is given by
Given a function 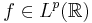 , the Lp space of integrable functions on the real line, then u can be understood as a harmonic extension of f into the upper half-plane. In analogy to the situation for the disk, when u is holomorphic in the upper half-plane, then u is an element of the Hardy space
, the Lp space of integrable functions on the real line, then u can be understood as a harmonic extension of f into the upper half-plane. In analogy to the situation for the disk, when u is holomorphic in the upper half-plane, then u is an element of the Hardy space 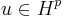 , and, in particular,
, and, in particular,
Thus, again, the Hardy space Hp on the upper half-place is a Banach space, and, in particular, a closed subspace of 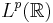 . The situation is only analogous to the case for the unit disk; the Lebesgue measure for the unit circle is finite, whereas that for the real line is not.
. The situation is only analogous to the case for the unit disk; the Lebesgue measure for the unit circle is finite, whereas that for the real line is not.
On the ball
For the ball of radius r, 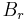 , in Rn, the Poisson kernel takes the form
, in Rn, the Poisson kernel takes the form
where 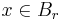 ,
, 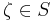 (the surface of
(the surface of 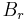 ), and
), and 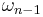 is the surface area of the unit sphere.
is the surface area of the unit sphere.
Then, if u(x) is a continuous function defined on S, the corresponding Poisson integral is the function P[u](x) defined by
It can be shown that P[u](x) is harmonic on the ball 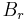 and that P[u](x) extends to a continuous function on the closed ball of radius r, and the boundary function coincides with the original function u.
and that P[u](x) extends to a continuous function on the closed ball of radius r, and the boundary function coincides with the original function u.
On the upper half-space
An expression for the Poisson kernel of an upper half-space can also be obtained. Denote the standard Cartesian coordinates of Rn+1 by
The upper half-space is the set defined by
The Poisson kernel for Hn+1 is given by
where
The Poisson kernel for the upper half-space appears naturally as the Fourier transform of the Abel kernel
in which t assumes the role of an auxiliary parameter. To wit,
In particular, it is clear from the properties of the Fourier transform that, at least formally, the convolution
is a solution of Laplace's equation in the upper half-plane. One can also show easily that as t → 0, P[u](t,x) → u(x) in a weak sense.
See also
References
- Conway, John B. (1978), Functions of One Complex Variable I, Springer-Verlag, ISBN 0-387-90328-3.
- Axler, S.; Bourdon, P.; Ramey, W. (1992), Harmonic Function Theory, Springer-Verlag, ISBN 0-387-95218-7.
- King, Frederick W. (2009), Hilbert Transforms Vol. I, Cambridge University Press, ISBN 978-0-521-88762-5.
- Stein, Elias; Weiss, Guido (1971), Introduction to Fourier Analysis on Euclidean Spaces, Princeton University Press, ISBN 0-691-08078-X.
- Weisstein, Eric W., "Poisson Kernel" from MathWorld.
- Gilbarg, D.; Trudinger, N., Elliptic Partial Differential Equations of Second Order, ISBN 3-540-41160-7.
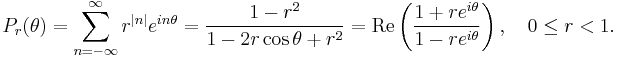
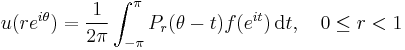
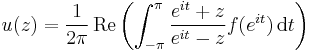
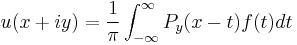
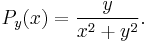

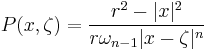
 = \int_S u(\zeta)P(x,\zeta)d\sigma(\zeta).\,](/2012-wikipedia_en_all_nopic_01_2012/I/975b7a757bd8dce843a3117328f6cf77.png)
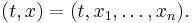
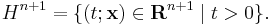
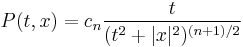
![c_n = \frac{\Gamma[(n%2B1)/2]}{\pi^{(n%2B1)/2}}.](/2012-wikipedia_en_all_nopic_01_2012/I/b0347bcfdb341fa118c388525277fb74.png)
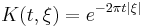
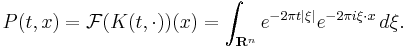
 = [P(t,\cdot)*u](x)](/2012-wikipedia_en_all_nopic_01_2012/I/b53f58befcaa089e859930102a69372a.png)